xz and multi-threading
What you (don't) need to know
I often use xz with the -T nn flag on my workstation when I have the CPU cores and RAM to spare it. I was under the assumption that I was paying for the gains in speed with something else—probably a worse deflation ratio. This has always been a longstanding assumption of mine, and it was time to put it to the test recently, when someone on IRC asked me if my assumption was correct.
Test I
I decided to start with a classic test for compression: attempting to compress pseudo-random data, and measuring the increase in file size. My motivation for this is that it is one extreme of the scale (the other being consistent data, all zeros for example). Extremes tend to show up edge cases.
I generated 8 GiB of pseudo-random data in tmpfs to help reduce the effect of any fragmentation problems increasing I/O overhead:
$ dd if=/dev/urandom of=/tmp/prandom bs=8G count=1 iflag=fullblock
2+0 records in
2+0 records out
8589934592 bytes (8.6 GB, 8.0 GiB) copied, 37.7439 s, 228 MB/s
Then, I compressed this file a number of separate times, with:
$ cd /tmp/
$ for thread in 1 2 4 6 8 10 16 24 32; do \
xz -9kv -T"$thread" prandom \
rm prandom.xz \
done
Here are the results:
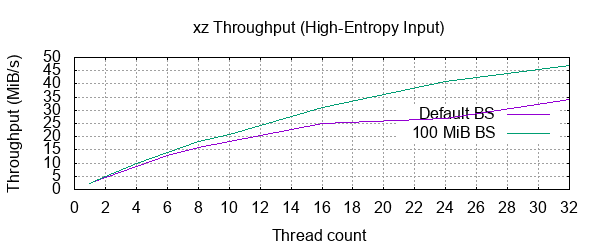
1: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 2.1 MiB/s 1:06:06
2: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 4.5 MiB/s 30:13
4: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 8.7 MiB/s 15:46
6: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 13 MiB/s 10:49
8: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 16 MiB/s 8:39
10: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 18 MiB/s 7:23
16: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 25 MiB/s 5:22
24: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 27 MiB/s 5:04
32: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 34 MiB/s 4:04
With a 100 MiB block size:
1: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 2.4 MiB/s 56:19
2: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 5.0 MiB/s 27:24
4: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 9.7 MiB/s 14:04
6: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 14 MiB/s 9:40
8: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 18 MiB/s 7:36
10: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 21 MiB/s 6:23
16: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 31 MiB/s 4:26
24: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 41 MiB/s 3:21
32: 100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 47 MiB/s 2:54
Diminishing returns when throwing more than a few threads at the job. This is because xz will share an input file among the threads by splitting it into chunks of data of a certain block size. This means that if the file size and block size are such that the total number of blocks is less than the number of threads we told it to use, it will simply use less threads.
Sure enough, reducing the block size to 100 MiB gives us a faster result. 100 MiB blocks would imply 81920 blocks, which should be enough to saturate a 32-thread machine. However, it's still not scaling as it "should". With 32 threads, we would ideally1 be seeing a 32-fold reduction in time over the single-threaded run, so about 2 minutes.
What happens if we reduce the block size to something silly: 10 MiB.
$ xz -9kv --block-size=10486760 -T32 prandom
prandom (1/1)
100 % 8,192.4 MiB / 8,192.0 MiB = 1.000 81 MiB/s 1:41
There's our (roughly) 2 minute guesstimate figure. We achieved the ideal performance, woohoo! But wait. What? This means that we just nearly doubled the throughput to 81 MiB/s, and didn't have any more inflation than normal. What sorcery is going on here? Let's try an even smaller block size.
$ xz -9kv --block-size=1048676 -T32 prandom
prandom (1/1)
100 % 8,192.7 MiB / 8,192.0 MiB = 1.000 83 MiB/s 1:38
Ahh there it is, and extra ~300 KiB of bloat added to the archive over and above our normal inflation. The changes in inflation were present earlier, but simply too small for the output from xz.
Weird. Let's try some other types of data.
Blank Space
Let's make some. Eight whatsits of it:
$ dd if=/dev/zero of=zeros bs=8G count=1 iflag=fullblock
1+0 records in
1+0 records out
8589934592 bytes (8.6 GB, 8.0 GiB) copied, 4.70468 s, 1.8 GB/s
Now compress it like we did earlier:
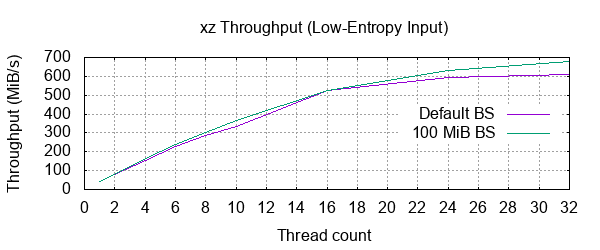
1: 100 % 1,220.3 KiB / 8,192.0 MiB = 0.000 40 MiB/s 3:27
2: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 82 MiB/s 1:40
4: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 156 MiB/s 0:52
6: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 227 MiB/s 0:36
8: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 286 MiB/s 0:28
10: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 335 MiB/s 0:24
16: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 527 MiB/s 0:15
24: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 596 MiB/s 0:13
32: 100 % 1,225.0 KiB / 8,192.0 MiB = 0.000 610 MiB/s 0:13
Much quicker on this run, and just look at those insignificant numbers. It does still look like the same behaviour from block size is biting us in the bum after the 4 thread mark. Let's retry with a 100 MiB block size:
1: 100 % 1,228.7 KiB / 8,192.0 MiB = 0.000 40 MiB/s 3:23
2: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 82 MiB/s 1:39
4: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 165 MiB/s 0:49
6: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 241 MiB/s 0:33
8: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 303 MiB/s 0:27
10: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 365 MiB/s 0:22
16: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 526 MiB/s 0:15
24: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 630 MiB/s 0:13
32: 100 % 1,229.3 KiB / 8,192.0 MiB = 0.000 677 MiB/s 0:12
Yikes! Much closer to our ideal, but still a ways off. The peak throughput is closer to the "ideal" 1.2 GiB/s, so perhaps with a larger input file it would show its speed better. Oh well. Looks like we gained just under 5 KiB when transitioning from single-threaded to multi-threaded. This might as well be zero.
This leaves the question down to less extreme data. Something that is commonly compressed with xz.
Big Booty Binaries
Let's get a bunch of built pacman packages, unxz them, tar them together, then try and compress this (roughly) 8 GiB file of all sorts - manpages, executables, configuration files, shared libraries, kernel images. All sorts of stuff junk.
Let's compress:
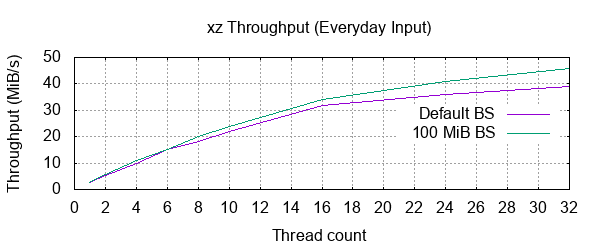
1: 100 % 1,608.7 MiB / 8,070.5 MiB = 0.199 2.7 MiB/s 50:18
2: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 5.3 MiB/s 25:33
4: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 10 MiB/s 12:49
6: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 15 MiB/s 9:07
8: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 18 MiB/s 7:23
10: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 22 MiB/s 6:02
16: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 32 MiB/s 4:14
24: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 36 MiB/s 3:44
32: 100 % 1,638.2 MiB / 8,070.5 MiB = 0.203 39 MiB/s 3:26
Let's retry the run again with a 100 MiB block size:
1: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 2.7 MiB/s 49:47
2: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 5.5 MiB/s 24:38
4: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 11 MiB/s 12:31
6: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 15 MiB/s 8:41
8: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 20 MiB/s 6:46
10: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 24 MiB/s 5:40
16: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 34 MiB/s 3:59
24: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 41 MiB/s 3:18
32: 100 % 1,651.2 MiB / 8,070.5 MiB = 0.205 46 MiB/s 2:54
Not bad, it appears to be a trend that going from single-threaded operations to any operation with more than one thread results in a very slight increase in the compressed file size, but this does not appear to scale up or down with the number of threads. That is to say, if you want to multi-thread a compression to optimise primarily for speed, you do not need to feel guilty that throwing, say, 8 threads at it rather than 2 is giving any worse a compression ratio.
TL;DR
Turns out the gains will most likely always far outweigh the (nearly immeasurable) decrease in compression ratio.
Footnotes
- I know, this isn't the perfect world and things don't quite scale linearly.